APPENDIX
SOME THOUGHTS ON THE MATHEMATICS OF THE INTERNAL FORCES IN THE DISC
The nucleus of an intervertebral disc is approximately a circle in horizontal section. It is an ellipse in vertical section. The computations involved in estimating the forces applied by such a figure are complex. However, it is valid, for our purpose, to regard the nucleus (Fig. 34) as a sphere, and also to regard the small free drop of jelly as a small sphere (Fig. 35).
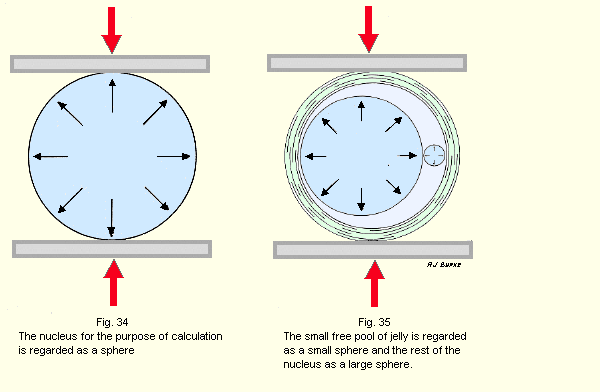
Then: The pressures exerted by the two spheres:
If
W = weight on vertebral body
D = diameter of the larger sphere
d = diameter of the smaller sphere
P = pressure exerted in pounds per square inch
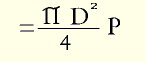
The pressure in the large sphere may be regarded as the same as in the nucleus:
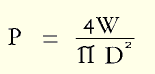
The radial force on the small sphere:
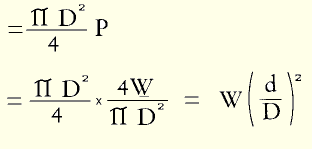
The pressure inside the small sphere is also P.
While very small the little sphere, with great pressure exerted equally on all areas of its circumference, acts as a solid. It bears on the inner surf ace of the annulus over a diameter g and pressure P per unit of surface area on the annulus is given by:
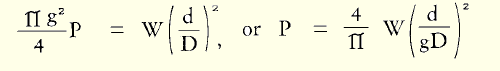
To this figure must be added the radial pressure exerted by the large sphere on the small sphere.
The small sphere behaves much like mercury which has been dropped on a clean glass surface. The minute drops are spherical. The larger volumes lie in flat pools.
SUMMARY
The small sphere exerts great pressure on a very small surface of the annulus. As it enlarges and flattens the pressure rapidly decreases,